1st Annual Brookfield Computer Programming Challenge
Congrats to all the teams who competed this year! Problem sets, an analysis of the problems,
problem solution code, solution videos, and final scores are all available here.
Congrats to all the teams who competed this year! Problem sets, an analysis of the problems, problem solution code, solution videos, and final scores are all available here.
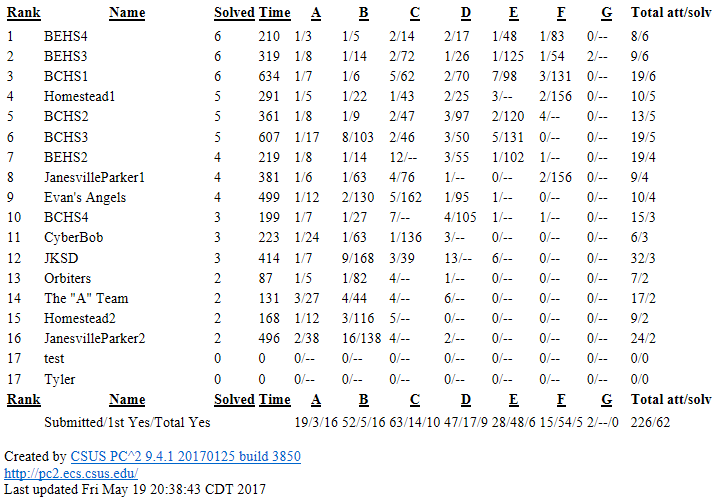
Final Standings
Congradulations to Brookfield East for placing 1st and 2nd, to Brookfield Central for placing 3rd, and to Homestead for placeing 4th! Also, congrats to all teams for being able to solve at least two problems!
Solution Videos
This is the introduction to the series.
Problem 1: Passing Bills. This was the input/output problem of the set. The problem consisted of inputting two numbers and printing the first of them.
Problem 2: Apple-Pen. This was the string manipulation problem of the set. This problem required knowledge of text input using the java.util.Scanner class, as well as string concatination (the '+' operator for Strings), and either the substring method or the split method.
Problem 3: The Halting Problem. This problem could have been solved in several ways, as discussed in the problem analysis. Valid solutions involved either using nested loops, or sorting and using a single loop.
For those of you who may be inclined to fact-check me, I misspoke in the beginning of the video. The Halting Problem was proved unsolvable by Alan Turing, not Charles Babbage. I must have seen the Babbage's name in the first line of the problem and accidentally said it instead.
Problem 4: One. This was the obligatory problem concerning the random mathmatical properties of an arbitrary number, in particular, the number 1. In addition to several other properties, 1 is the only natural number that is neither prime nor composite, so this problem required a program that could efficiently find whether a number was prime, composite, or neither. Because the input was very large, however, this required the program to be efficient in choosing which numbers to check.
Problem 5: Negligent Norbert. This was the mathematical problem of the set, which required a program to efficiently count the minimum number of keystokes to type a given number of unique responses to clarification requests to a programming competition.
Problem 6: Calculatus Eliminatus. This problem involved finding the location of a missing object by eliminating all of the places it couldn't be. One solution was based on a decrease-and-conquere approach and involved combining ranges that werea adjacent to each other, while the another valid solution was based on the properties of ranges once they had been sorted in a certain manner.
Problem 7: Bike Race. This was a graph theory problem that required finding the diameter of a graph. The algorythm used in the video and problem analysis is known as the Floyd-Warshal algorythm, which along with Dijkstra's algortyhm is incredibly helpful for solving most graph theory problems. While several teams got quite close, no teams were able to submit a correct solution to this problem during the competition.
Bonus Problem: LAST Robotics. This was the bonus problem of the set, which was only available to teams who solved the other problems before hand. This problem involved knowledge of either binary numbers or a nifty recursive discovery.